数据结构 : 树
树的基本概念
- 结点
- 根结点
- 父结点(双亲结点)
- 子结点(孩子结点)
- 子树
- 空树
- 度:一个结点,拥有的子树数(结点有多少分支)
- 层次:从一棵树的树根开始,树根所在层为第一层,根的孩子结点所在的层为第二层
- 有序树和无序树:树中结点的子树从左到右,谁在左,谁在右,若有规定,则这棵树称为有序树;反之称为无序树
- 森林:由 m(m >= 0)个互不相交的树组成的集合被称为森林,简单理解就是当根结点有多个子树时,他们的子树在一起就是森林
二叉树
- 普通二叉数
- 定义
子节点有0,1,2个的数,没啥好说的
- 满二叉树
- 定义
除了叶子结点,所有结点都有两个子结点的树 - 特性

3. 完全二叉树
- 定义
除了叶子结点,所有结点都有两个子结点的树,且叶子结点必须按照从左到右的顺序依次有值,数量>=1 - 特性

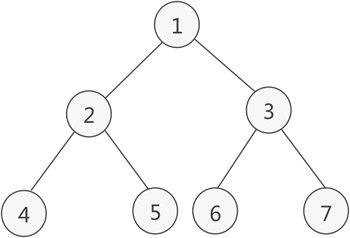
4. 二叉树遍历算法
- 层次遍历
每一层从左到右依次输出
1234567 - 先序遍历
每遇到一个节点,先访问,然后再遍历其左右子树
1245367 - 中序遍历
第一次经过时不访问,等遍历完左子树之后再访问,然后遍历右子树
4251637 - 后序遍历
第一次和第二次经过时都不访问,等遍历完该节点的左右子树之后,最后访问该节点
4526731 - 参考练习图
哈夫曼树
- 定义及用处
- 定义
当用 n 个结点(都做叶子结点且都有各自的权值)试图构建一棵树时,如果构建的这棵树的带权路径长度最小,称这棵树为“最优二叉树”,有时也叫“赫夫曼树”或者“哈夫曼树” - 用途
构造最优编码,用于信息传输,数据压缩等方面。参考第四点,哈夫曼编码
- 相关概念了解
- 路径:在一棵树中,一个结点到另一个结点之间的通路,称为路径
- 路径长度:在一条路径中,每经过一个结点,路径长度都要加 1
- 结点的权:给每一个结点赋予一个新的数值,被称为这个结点的权
- 结点的带权路径长度:指的是从根结点到该结点之间的路径长度与该结点的权的乘积
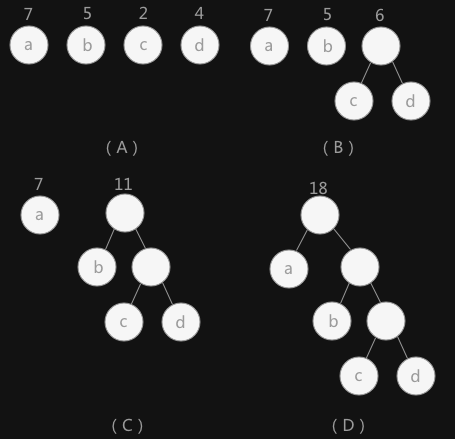
- 构建哈夫曼树的过程
- 特点:从叶子结点开始构建
对于给定的有各自权值的 n 个结点,构建哈夫曼树有一个行之有效的办法: - 在 n 个权值中选出两个最小的权值,对应的两个结点组成一个新的二叉树,且新二叉树的根结点的权值为左右孩子权值的和;
- 在原有的 n 个权值中删除那两个最小的权值,同时将新的权值加入到 n–2 个权值的行列中,以此类推;
- 重复 1 和 2 ,直到所以的结点构建成了一棵二叉树为止,这棵树就是哈夫曼树。
4. 哈夫曼编码
- 目的及用途
信息传输和数据压缩 - 方法
将字符串转为二进制,且每个字符的编码都不能由其他字母的编码组成 - 步骤
- 将数据进行拆分成多个最小颗粒度,且统计每个最小颗粒度的数量(权重)
- 按照第三点:构建哈夫曼树的过程,构建哈夫曼树
- 构建出的哈夫曼树,其左叶子结点标记为0,右叶子结点标记为1
- 每个最小颗粒度的编码为跟结点至其的标记连接(可以理解成字符串链接)
- 举例说明
- 字符串 : abbcccdddd
- 拆分 : a权重 : 1;b权重 : 2;c权重 : 3;d权重 : 4;
- 构建哈夫曼数,得到标记 : a标记 : 1111;b标记 : 1110;c标记 : 110;d标记 : 10;
- 用标记来来拼接连成字符串
- 最终可得字符串的二进制 : 11111110111011011011010101010
回溯算法
- 实现过程(通过状态树实现)
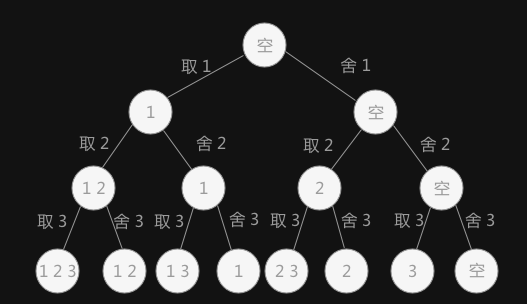
- 常用解决八皇后问题
